Video: Je po částech lineární funkce?
2024 Autor: Miles Stephen | [email protected]. Naposledy změněno: 2023-12-15 23:34
A po částech lineární funkce je funkce složený z nějakého počtu lineární segmenty definované ve stejném počtu intervalů, obvykle stejné velikosti.
Co je tímto způsobem po částech lineární model?
Tato aproximace Modelka ve kterém ne lineární zařízení se chová jako a lineární jeden pro určitý rozsah napětí se nazývá po částech lineární model z ne lineární přístroj. Jeho I-V charakteristika je podobná jako u a lineární odpor, to znamená, že jeho napětí roste lineárně s nárůstem jeho proudu.
Také, co je to po částech? A po částech -definovaná funkce je taková, která není definována jedinou rovnice , ale o dva nebo více. Každý rovnice platí pro určitý interval.
Když to vezmeme v úvahu, co je příklad po částech?
A po částech je funkce který je definován na posloupnosti intervalů. Běžný příklad je absolutní hodnota, (1) Funkce po částech jsou implementovány v jazyce Wolfram as Po částech [val1, kond1, val2, kond2,].
Co je rodičovská funkce absolutní hodnoty?
An funkce absolutní hodnoty je funkce který obsahuje algebraický výraz uvnitř absolutní hodnota symboly. Připomeňme, že absolutní hodnota čísla je jeho vzdálenost od 0 na číselné ose. The absolutní hodnota rodičovské funkce , zapsaný jako f(x)=| x |, je definováno jako. f(x)={x, pokud x>00, pokud x=0−x, pokud x<0.
Doporučuje:
Je funkce lineární nebo nelineární?
Lineární funkce je funkce se standardním tvarem y = mx + b, kde m je sklon ab je průsečík y a jejíž graf vypadá jako přímka. Existují další funkce, jejichž graf není přímka. Tyto funkce jsou známé jako nelineární funkce a přicházejí v mnoha různých formách
Co je příklad po částech?
Po částech je funkce vytvořená z částí různých funkcí v různých intervalech. Například můžeme vytvořit funkci po částech f(x), kde f(x) = -9, když -9 < x ≦ -5, f(x) = 6, když -5 < x ≦ -1, a f(x) = -7, když -1 <x ≦ 9
Mají všechny lineární funkce inverze?
Inverze k nekonstantním lineárním funkcím. Lineární funkce bude invertibilní, pokud bude nekonstantní, nebo jinými slovy bude mít nenulový sklon. Inverzi můžete najít buď algebraicky, nebo graficky odrazem původní čáry přes úhlopříčku y = x
Jak transformujete lineární funkce?
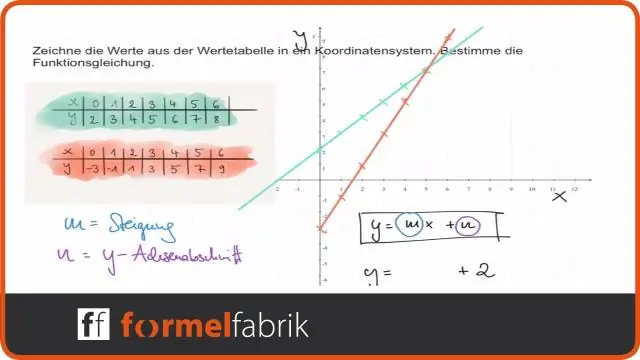
Jak na to: Vzhledem k rovnici lineární funkce použijte transformace ke grafu lineární funkce ve tvaru f(x)=mx+b f (x) = m x + b. Graf f(x)=x f (x) = x. Vertikálně roztáhněte nebo zmáčkněte graf o faktor |m|. Posun grafu nahoru nebo dolů b jednotek
Jak poznáte, že po částech graf je funkce?
Jak zjistit, zda je funkce po částech spojitá nebo nespojitá. Chcete-li zjistit, zda je graf po částech spojitý nebo nesouvislý, můžete se podívat na hraniční body a zjistit, zda je bod y v každém z nich stejný. (Pokud by byla y různá, došlo by v grafu ke „skoku“!)