Video: Jak najdete další člen v kvadratické posloupnosti?
2024 Autor: Miles Stephen | [email protected]. Naposledy změněno: 2023-12-15 23:34
Zapište n-tý období z toho kvadratický číslo sekvence . Krok 1: Potvrďte, zda je sekvence je kvadratický . To se provádí nalezením druhého rozdílu. Krok 2: Pokud vydělíte druhý rozdíl 2, dostanete hodnotu a.
Podobně, jaký je vzorec pro nalezení n-tého členu v posloupnosti?
Takový sekvence lze vyjádřit v termínech n-tý termín z sekvence . V tomto případě je n-tý termín = 2n. Na nalézt 1 období , vložte n = 1 do vzorec , do nalézt 4 období , nahraďte n číslicemi 4: 4 období = 2 × 4 = 8.
Dále, jak zjistíte kvadratickou posloupnost? O kvadratických posloupnostech
- První člen je a × 1 2 + b × 1 + c = a + b + c.
- Druhý člen je a × 2 2 + b × 2 + c = 4 a + 2 b + c.
- Třetí člen je a × 3 2 + b × 3 + c = 9 a + 3 b + c.
Víte také, co je n-tý člen posloupnosti?
' n-tý ' období je vzorec s 'n' v něm, který vám umožňuje najít jakékoli termín sekvence aniž byste museli z jednoho stoupat období další. 'n' znamená období číslo, abyste našli 50 období jen bychom ve vzorci nahradili 50 místo 'n'.
Co je kvadratická rovnice v matematice?
A kvadratická rovnice je rovnice druhého stupně, což znamená, že obsahuje alespoň jeden výraz na druhou. Standardní tvar je ax² + bx + c = 0, přičemž a, b a c jsou konstanty nebo číselné koeficienty a x je neznámá proměnná.
Doporučuje:
Jak vypadá graf kvadratické rovnice?
Grafem kvadratické funkce je křivka ve tvaru U nazývaná parabola. Lze jej nakreslit vynesením řešení rovnice, nalezením vrcholu a pomocí osy symetrie vynesením vybraných bodů nebo nalezením kořenů a vrcholu. Standardní tvar kvadratické rovnice je
Jak najdete symbolickou reprezentaci kvadratické funkce?
Kvadratické funkce lze symbolicky znázornit rovnicí y(x) = ax2 + bx + c, kde a, b a c jsou konstanty a a ≠ 0. Tento formulář se označuje jako standardní formulář
Jak najdete a v kvadratické funkci?
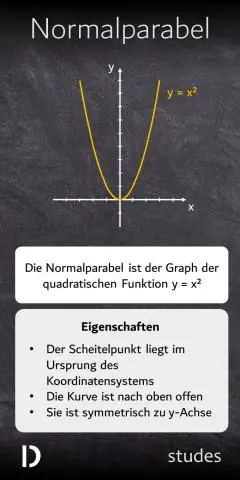
Kvadratická funkce f(x) = a(x -h)2 + k, a nerovná se nule, je považována za standardní. Pokud je a kladné, otevře se graf směrem nahoru, a pokud je a záporné, otevře se směrem dolů. Čára symetrie je svislá přímka x = h a vrchol je bod (h,k)
Jak najdete další číslo v řadě?
Nejprve najděte společný rozdíl pro sekvenci. Odečtěte první termín od druhého termínu. Odečtěte druhý termín od třetího termínu. Chcete-li najít další hodnotu, přidejte k poslednímu danému číslu
Jaké jsou vzorce pro aritmetické a geometrické posloupnosti?
Pokud se podíváte do jiných učebnic nebo online, možná zjistíte, že jejich uzavřené vzorce pro aritmetické a geometrické posloupnosti se liší od našich. Konkrétně můžete najít vzorce an=a+(n−1)d a n = a + (n − 1) d (aritmetika) a an=a⋅rn−1 a n = a ⋅ r n − 1 (geometrické)