
- Autor Miles Stephen [email protected].
- Public 2023-12-15 23:34.
- Naposledy změněno 2025-06-01 05:04.
Jen si představte 2x2 matice to znamená podobně jako jeho inverzní aniž by byly diagonální položky 1 nebo -1. Úhlopříčka matrice udělám. Takže A a inverzní z A are podobný , takže jejich vlastní hodnoty jsou stejné. je-li jedno z vlastních čísel A n, a vlastních čísel jeho inverzní bude 1/n.
Také se zeptal, je matice podobná její transpozici?
Jakýkoli čtverec matice přes pole je podobný jeho transpozici a jakýkoli čtvercový komplex matice je podobný do symetrického komplexu matice.
Podobně jsou všechny invertibilní matice podobné? Pokud jsou A a B podobný a invertibilní , pak jsou A-1 a B-1 podobný . Důkaz. Od té doby Všechno a matrice jsou invertibilní , můžeme vzít obrácenou hodnotu obou stran: B-1 = (P-1AP)-1 = P-1A-1(P-1)-1 = P-1A-1P, takže A-1 a B-1 jsou podobný . Pokud jsou A a B podobný , stejně jako Ak a Bk pro libovolné k = 1, 2,.
Pokud jde o toto, může být matice podobná sama sobě?
Tedy Any matice je sobě podobný : I−1AI=A. Pokud je A podobný k B, pak B je podobný do A: pokud B=P−1AP, pak A=PBP−1=(P−1)−1BP−1. Pokud je A podobný do B přes B=P−1AP a C je podobný do B přes C=Q−1BQ, pak A je podobný do C: C=Q−1P−1APQ=(PQ)−1APQ.
Co to znamená, když jsou matice podobné?
V lineární algebře dvě n-na-n matrice A a B se nazývají podobné pokud existuje invertibilní n-by-n matice P takové, že. Podobné matrice představují stejnou lineární mapu pod dvěma (možná) různými bázemi, přičemž P je změna báze matice.
Doporučuje:
Co je optimalizace Hessovy matice?
Použití při optimalizaci Hessovské matice se používají ve velkých optimalizačních problémech v rámci metod Newtonova typu, protože jsou koeficientem kvadratického členu lokálního Taylorova rozšíření funkce
Co jsou matice v diskrétní matematice?
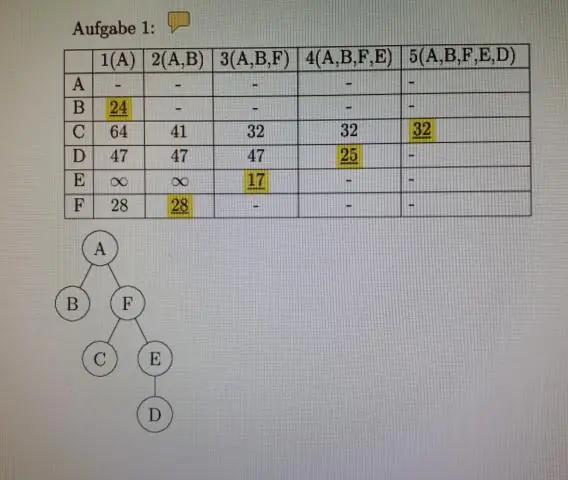
Diskrétní matematika a její aplikace Poznámky ke kapitole 2 2.6 Snímky z přednášek Matice Autor Adil Aslammailto:[email protected]. Definice matice •Matice je pravoúhlé pole čísel. Matice s m řádky a n sloupci se nazývá matice m x n. Množným číslem matice jsou matice
Co je kanonická matice?

Kanonická forma. Technika, která se používá k reprezentaci matematických entit nebo matice v jejich standardní formě (nebo matematickém vyjádření), se nazývá kanonická forma. Trojúhelníková forma, Jordanova kanonická forma a forma řady jsou některé hlavní kanonické formy v lineární algebře
Jak zjistíte aditivní inverzi matice?

K získání aditivní inverze dané matice stačí vynásobit každý prvek matice -1. Když vynásobíme každý prvek matice -1, stane se roven -A. A+(-A) se tedy rovná 0, kde 0 je nulová matice. Splňuje základní definici aditivní inverze
Jak násobíte matice na grafické kalkulačce?

Krok 1: Zadejte první matici do kalkulačky. Chcete-li zadat matici, stiskněte [2ND] a [x−1]. Krok 2: Zadejte druhou matici do kalkulačky. Stiskněte [2ND] a [x−1]. Krok 3: Stisknutím [2ND] a [MODE] opustíte maticovou obrazovku. Krok 4: Vyberte matici A a matici B v nabídce NAMES a vyhledejte produkt
