Video: Existuje uzavírací vlastnost odčítání, která se vztahuje na celá čísla?
2024 Autor: Miles Stephen | [email protected]. Naposledy změněno: 2023-12-15 23:34
Uzavření je matematický vlastnictví související sady čísla a operace. Pokud operace na kterýchkoli dvou čísla v sadě produkuje a číslo který je v sadě, máme uzavření . Zjistili jsme, že soubor celá čísla není uzavřen pod odčítání , ale množina celých čísel je uzavřena pod odčítání.
Existuje zde uzavírací vlastnost odečítání?
Uzavření nemovitosti Když se jedno celé číslo odečte od druhého, a rozdíl není vždy celé číslo. Tohle znamená tamto a celá čísla nejsou uzavřena pod odčítání.
Také, co to znamená být uzavřen pod odečítáním? Uzavření je, když operace (například "sčítání") na členech množiny (například "reálná čísla") vždy dělá členem stejné množiny. Takže výsledek zůstane ve stejné sadě.
Podobně se ptá, je odčítání uzavřeno pro celá čísla?
Celá čísla : Tato sada je Zavřeno pouze při sčítání a násobení. Celá čísla: Tato množina je Zavřeno pouze pod dodatkem, odčítání , a násobení. Racionální Čísla : Tato sada je Zavřeno pod přidáním, odčítání , násobení a dělení (s výjimkou dělení 0).
Jaký je příklad uzavírací vlastnosti?
Uzavření nemovitosti . The uzavírací vlastnost znamená, že množina je uzavřena pro nějakou matematickou operaci. Pro příklad , množina sudých přirozených čísel, [2, 4, 6, 8,…], je s ohledem na sčítání uzavřený, protože součet libovolných dvou z nich je dalším sudým přirozeným číslem, které je také členem množiny.
Doporučuje:
Jsou celá čísla vždy někdy nebo nikdy racionální čísla?
1,5 je racionální číslo, které lze zapsat jako: 3/2 kde 3 a 2 jsou celá čísla. Zde je racionální číslo 8 celé číslo, ale racionální číslo 1,5 není celé číslo, protože 1,5 není celé číslo. Můžeme tedy říci, že racionální číslo je celé číslo, někdy ne vždy. Správná odpověď je tedy někdy
Co jsou přirozená čísla celá čísla celá čísla a racionální čísla?
Reálná čísla se dělí hlavně na racionální a iracionální čísla. Racionální čísla zahrnují všechna celá čísla a zlomky. Všechna záporná a celá čísla tvoří množinu celých čísel. Celá čísla se skládají ze všech přirozených čísel a nuly
Existuje identitní vlastnost odečítání?
Co je vlastnost identity? Navíc a odčítání je identita 0. Při násobení a dělení je identita 1. To znamená, že když se k n přičte nebo odečte 0, pak n zůstane stejné
Jsou některá iracionální čísla celá čísla?
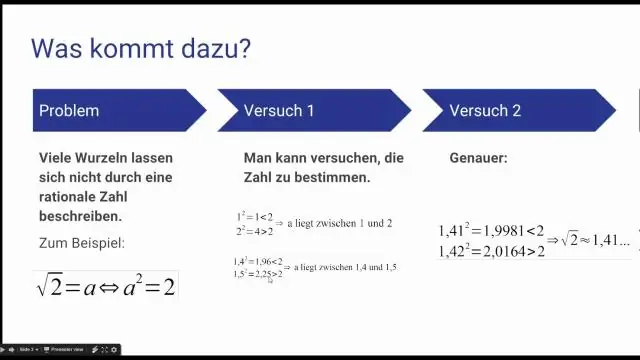
Odpověď a vysvětlení: Iracionální čísla nejsou celá čísla. Iracionální číslo je číslo, které není racionální. Jinými slovy, iracionální číslo nelze napsat
Co jsou to celá čísla a racionální čísla Jak jsou body zakresleny v souřadnicové rovině?
Jak jsme řekli, body na souřadnicové rovině jsou reprezentovány jako (a, b), kde a a b jsou racionální čísla. Racionální čísla jsou čísla, která lze zapsat jako zlomek, p/q, kde p a q jsou celá čísla. A nazýváme x-ovou souřadnicí bodu a b nazýváme y-ovou souřadnicí bodu