Video: Jak vyřešíte rovnici izolováním proměnné?
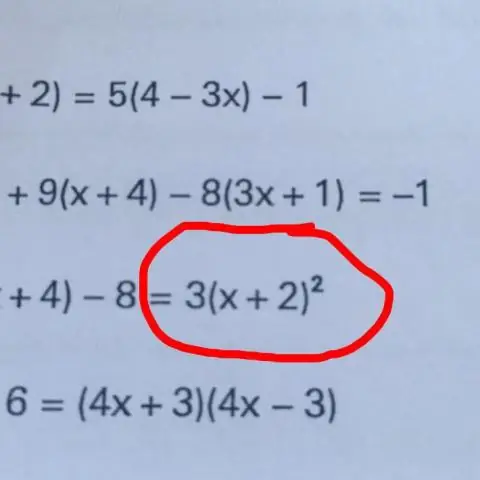
2024 Autor: Miles Stephen | [email protected]. Naposledy změněno: 2023-12-15 23:34
Základní technika k izolovat A variabilní je „udělat něco pro obě strany“. rovnice , jako je sčítání, odečítání, násobení nebo dělení obou stran rovnice stejným číslem. Opakováním tohoto procesu můžeme získat proměnná izolovaná na jedné straně rovnice.
Co je tedy vzorec v matematice?
Definice a vzorec je skupina matematický symboly, které vyjadřují vztah nebo které se používají k řešení problému nebo způsobu, jak něco vytvořit. Skupina matematika symboly, které vyjadřují vztah mezi obvodem kruhu a jeho průměrem, je příkladem a vzorec.
Podobně, co myslíte proměnnou? V programování a variabilní je hodnota, která umět měnit v závislosti na podmínkách nebo na informacích předávaných programu. Typicky se program skládá z instrukcí, které říkají počítači, co má dělat a data, která program používá, když je spuštěn.
Podobně, co je doslovná rovnice?
A doslovná rovnice je rovnice kde proměnné představují známé hodnoty. Doslovné rovnice umožňují použití reprezentovat věci jako vzdálenost, čas, zájem a sklon jako proměnné v an rovnice . Používání proměnných místo slov skutečně šetří čas!
Co jsou koeficienty?
V matematice a součinitel je multiplikativní faktor v nějakém termínu polynomu, řady nebo jakéhokoli výrazu; je to obvykle číslo, ale může to být jakýkoli výraz. Například, pokud je y považováno za parametr ve výše uvedeném výrazu, je součinitel z x je -3y a konstanta součinitel je 1,5 + r.
Doporučuje:
Jak vyřešíte kvadratickou rovnici pomocí zákona nulového faktoru?
Z toho můžeme usoudit, že: Pokud je součin jakýchkoli dvou čísel nula, pak jedno nebo obě čísla jsou nula. To znamená, že pokud ab = 0, pak a = 0 nebo b = 0 (což zahrnuje možnost, že a = b = 0). Toto se nazývá zákon nulového faktoru; a často jej používáme k řešení kvadratických rovnic
Jaké jsou proměnné v Bernoulliho rovnici?
Proměnné P 1 P_1 P1?P, počáteční index, 1, koncový index, v 1 v_1 v1?v, počáteční index, 1, koncový index, h 1 h_1 h1?h, počáteční index, 1, koncový index, odkazují na tlak , rychlost a výška tekutiny v bodě 1, zatímco proměnné P 2 P_2 P2?P, počáteční index, 2, koncový index, v 2 v_2 v2?v, začátek
Jak algebraicky vyřešíte rovnici absolutní hodnoty?
ŘEŠENÍ ROVNIC OBSAHUJÍCÍ ABSOLUTNÍ HODNOTY Krok 1: Izolujte výraz absolutní hodnoty. Krok 2: Nastavte veličinu v zápisu absolutní hodnoty rovnající se + a - veličině na druhé straně rovnice. Krok 3: Řešte neznámou v obou rovnicích. Krok 4: Zkontrolujte svou odpověď analyticky nebo graficky
Jak vyřešíte rovnici lineární nerovnosti?
Existují tři kroky: Uspořádejte rovnici tak, aby 'y' bylo vlevo a vše ostatní vpravo. Nakreslete čáru 'y=' (udělejte z ní plnou čáru pro y≤ nebo y≥ a přerušovanou čáru pro y) Stínujte nad čáru pro 'větší než' (y> nebo y≥) nebo pod čáru pro a 'menší než' (y< nebo y≤)
Jak vyřešíte lineární rovnici pomocí Gaussovy eliminace?
Jak používat Gaussovu eliminaci k řešení soustav rovnic Jakýkoli řádek můžete vynásobit konstantou (jinou než nulou). vynásobí řádek tři číslem –2, čímž získáte nový řádek tři. Můžete přepínat libovolné dva řádky. prohodí řádky jedna a dva. Můžete přidat dva řádky dohromady. sečte řádky jedna a dva a zapíše to do řádku dva