- Autor Miles Stephen [email protected].
- Public 2023-12-15 23:34.
- Naposledy změněno 2025-06-01 05:04.
Ve statistikách 68 - 95 - pravidlo 99,7 , také známý jako empirický pravidlo , je zkratka použitý zapamatovat si procento hodnot, které leží v pásmu kolem průměru v normálním rozdělení o šířce dvou, čtyř a šesti směrodatných odchylek; přesněji, 68,27 %, 95,45 % a 99,73 % hodnot leží
Jaké je v tomto ohledu pravidlo 95 procent?
Empirický pravidlo uvádí, že pro normální rozdělení budou téměř všechna data spadat do tří standardních odchylek od průměru. 95 % spadá do dvou směrodatných odchylek. 99,7 % spadá do tří standardních odchylek.
Také víte, jaké jsou 68% 95% a 99,7% intervaly spolehlivosti pro průměr vzorku? Od té doby 95 % hodnot spadá do dvou směrodatných odchylek znamenat podle 68 - 95 - 99.7 Pravidlo, jednoduše sečtěte a odečtěte dvě směrodatné odchylky od znamenat za účelem získání 95 % interval spolehlivosti . Podle 68 - 95 - 99.7 Pravidlo: ➢ The 68 % interval spolehlivosti pro tohle příklad je mezi 78 a 82.
Také je třeba vědět, proč je standardní odchylka 68 procent?
Jak řekli jiní, je to výsledek počtu, který tento vzorec vypočítal jako integrál od -1/2 sigma do 1/2 sigma (pokrývající 1 sigma = 1 standardní odchylka ) výsledkem je plocha pod křivkou 0,68, přičemž celá plocha vypočítaná jako integrál od -nekonečna do +nekonečna je 1, takže dostanete 68 % pro jeden standard
Co je 95procentní interval spolehlivosti?
A 95 % interval spolehlivosti je rozsah hodnot, kterými můžete být 95 % jistý obsahuje skutečný průměr populace. S malým vzorkem vlevo, 95 % interval spolehlivosti je podobný rozsahu dat.
Doporučuje:
Jak používáte pravidlo součinu a podílu?

Pravidlo součinu říká, že derivace součinu dvou funkcí je první funkce krát derivace druhé funkce plus druhá funkce krát derivace první funkce. Produktové pravidlo se musí použít, když se má vzít derivace podílu dvou funkcí
Jak vyřešíte pravidlo exponentu?
Posouvejte pouze záporné exponenty. Produktové pravidlo: am ∙ an = am + n, to říká, že pro vynásobení dvou exponentů se stejným základem ponecháte základ a sečtete mocniny., to říká, že pro dělení dvou exponentů se stejným základem ponecháte základ a odečíst pravomoci
Jak víte, kdy použít pravidlo součinu nebo podílu?

Dělení funkcí. Takže kdykoli uvidíte násobení dvou funkcí, použijte pravidlo součinu a v případě dělení použijte pravidlo podílu. Pokud má funkce násobení i dělení, použijte odpovídajícím způsobem obě pravidla. Pokud vidíte obecnou rovnici, je to něco jako,, kde je funkce z hlediska samotné
Jak používáte pravidlo pravé ruky pro křížový produkt?
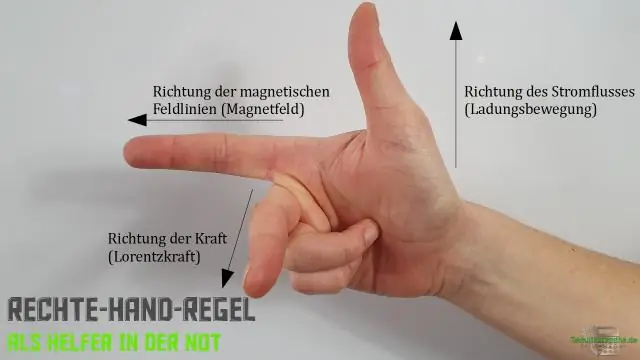
Pravidlo pravé ruky říká, že orientace křížového součinu vektorů je určena umístěním a ocasem k ocasu, zploštěním pravé ruky, jejím natažením ve směru a následným svinutím prstů ve směru, se kterým svírá úhel. Palec pak ukazuje ve směru
Jak převedete pravidlo podílu na pravidlo produktu?

Kvocientové pravidlo lze chápat jako aplikaci pravidel produktu a řetězce. Jestliže Q(x) = f(x)/g(x), pak Q(x) = f(x) * 1/(g(x)). K rozlišení Q(x) můžete použít pravidlo součinu a 1/(g(x)) lze odlišit pomocí řetězového pravidla s u = g(x) a 1/(g(x)) = 1/u
